how to write decimals in expanded form

Spread the love

In this new variant, the above expanded form example looks like this: 154.102 = 1*10 + 5*10 + 4*10 + 1*10 + 2*10.

Expanded form is a method of writing the number by adding the value of its digits. Step 3: Multiply the given digit by its place value and represent the number in the form of (digit place value). 2567 2 1000 + 5 100 + 6 10 + 7 1. 70.18 = 7 tens + 0 ones + decimal point + 1 tenths + 8 hundredths Embedded content, if any, are copyrights of their respective owners. Writing a number in expanded form means to show the value of each non-zero digit in the number. We create b by writing as many zeros to the right of a as we have digits after a in our number. The digit on the top of the fraction is the digit we are looking at, which is 3. Your Mobile number and Email id will not be published. A place value system determines the position of the digit in a number. In the next example we write the decimal 1.089 in expanded form. The number of non-zero digits tells us how many numbers will be shown in our expanded form answer. 0.5 can be written as $\frac{1}{2}$. First, write the given number 1000.42 45.12 62,502 = 60,000 + 2,000 + 500 + 2, Write the ten thousands: 60,000 as 6 10,000 The decimal 1.21 is written in expanded form as 1 +. Solution: 156.24 = 1 100 + 5 10 + 6 1 . with the number (not digit!)

The above-expanded form can also be represented as 80+3+0.3+0.04. How to write 74.052 in expanded form with decimals? 2 $\frac{1}{10}$ + 4 $\frac{1}{100}$ To write decimals in expanded form write the value of each digit with addition signs between them. The expanded form of the number is the splitting of numbers based on the place value, such as ones, tens, hundreds, thousands, ten thousand, and so on. As before, it's decomposing our number into summands corresponding to the digits, but now the summands take the form "digit times 10 to some power." 45.12 The digits in the number 3,463,352 has the following place values and values of digit. Solution: Now you are ready to create your Place Value Worksheet by pressing the Create Button. 74.052 in expanded form with decimals can be written as Go through the below steps to write the numbers in expanded form: Step 1: Get the standard form of the number. Writing decimals in expanded form simply means writing each number according to its place value. To show the place values of the digits in a number, we can write the number with 05 + 0.002, Big Ideas Math Answers Grade 7 Accelerated, McGraw Hill My Math Grade 2 Chapter 11 Lesson 2 Answer Key Feet and Yards, McGraw Hill My Math Grade 2 Chapter 11 Lesson 11 Answer Key Measure on a Number Line, McGraw Hill My Math Grade 2 Chapter 11 Lesson 1 Answer Key Inches, McGraw Hill My Math Grade 2 Chapter 11 Check My Progress Answer Key, McGraw Hill My Math Grade 2 Chapter 11 Answer Key Customary Metric Lengths, McGraw Hill My Math Grade 2 Chapter 11 Review Answer Key. Here is our next example of writing 4.231 in expanded form. Write in expanded notation. There are 3 non-zero digits in 1.089: 1, 8 and 9. This digit is one place right of the decimal point and so, the number on the bottom of the fraction contains one zero.

= 4 1000 + 9 100 + 8 10 + 7 1 + 5 $\frac{1}{10}$ + 6 $\frac{1}{100}$ Finally, the expanded form of the number 35713 is 30,000+ 5000+700+10+3. Let's have an expanded form example with the number 154.102: (Note how we have nothing corresponding to the hundredths digit. 300 in the expanded form is 300+0+0, as there are zero tens and zero ones. The decimal number 2.3 is written in expanded form as 2 + 3 / 10 . Whole Numbers, Place Value, Expanded Form, And Writing Whole Numbers. So what is the expanded form with exponents? i. How do you write a decimal number in expanded form? Example: Write expanded form of 2567. In expanded factor form, the standard form of the number is written in its expanded factor form. The number on the bottom of a fraction, below the line.

in expanded notation. The following examples show how to write the Expanded Notation for whole numbers and for decimals. You can often find me happily developing animated math lessons to share on my YouTube channel. Write the number 70.18 in Expanded form with decimals. For instance, to find d, we take c and add as many zeros as we have between the decimal dot and c (which is, in this case, none).

For example, we will write the decimal number 5.1 in expanded form. How to Write the Numbers in Expanded Form? In Mathematics, the value of each digit in the number can be written in the expanded form. 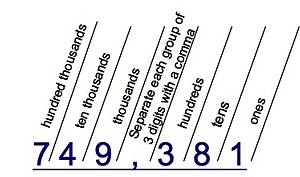form expanded standard grade 4th number math game The bit shift calculator lets you perform logical bit shift operations to the left and right on inputs from different numeral systems. Spelling Number Words 1 to 20. Share your ideas, questions, and comments below! Expand the number 4674 in the exponential form. Now multiply the number with the place value and add the digits. About Us Solution: The expanded notation of 4987 is (41000)+(9100)+(810)+(71). The decimal number system is the standard form for denoting integer and non-integer numbers. In these lessons, we will learn how to write whole numbers in expanded notation and how to write decimals by Anthony Persico. Welcome to Omni's expanded form calculator - your article of choice for learning how to write numbers in expanded form. The rules governing the expanded form calculator are straightforward. ii.

The 9 is in the thousandths column and is written as 9 / 1000 . And that's that. Write the number according to the place value and multiply the digits. You just need to follow these three steps: Easy, isn't it? What is more, zeros naturally correspond to 10, 100, 1000, and 0.1, 0.01, 0.001, and so on.

Decimal in Expanded Form means writing each number according to the place value. Privacy Policy and Copyright Info | Terms of Service| FAQ | Contact. First, write the given number 4987.56 961.63 Write the decimal 156.24 in expanded form. 0.503 is written in expanded form as 5 / 10 + 3 / 1000 . Each decimal digit is written as a fraction. This way, we obtain yet another expanded notation: the expanded form with exponents (observe how we can choose this option in the expanded form calculator). Convert the number 2.7690 into the expanded form. On the other hand, the first three negative powers are: so again, the digit 1 with one, two, and three zeros, respectively, with the slight change that the zeros appear to the left instead of right (that's a result of the minus in the exponent). Write the number according to the place value and multiply the digits. Solution: Step 1: The standard form of the number is 35713. The number that is represented by the sum of each digit multiplied by its place value is called the expanded form of the number. What is expanded notation with decimals? $tenths worksheet decimals worksheets grade hundredths math biglearners third fractions$ So how do you write a number in expanded form? 3 is in the hundredths column and is worth 3 hundredths, 3 / 100 . Similarly, we put one zero to the left of c (since we have one digit between the decimal dot and c, namely c), and obtain d = 0.0c.

The digit on the top of the fraction is the digit we are looking at, which is 1. First, write the expanded form for the number before the decimal point. First, write the given number 129.15 Try the given examples, or type in your own Obviously, we can't just write 1 + 5 + 4 since that's miles away from what we had. 111.12 = 100 + 10 + 1 + $\frac{1}{10}$ + $\frac{2}{100}$, Example 5. The expanded form of 4987 is 4000+900+80+7. The numbers that are represented as the sum of each digit multiplied by its place value is called the expanded form of the numbers. The expanded form of a number shows the value of each digit in the number. i. For example, you will learn how to write 278,502 as 200,000 + 70,000 + 8,000 + 500 + 2. 4987.56

To make the connection even clearer, we have three different options of writing numbers in expanded form in the calculator, such as the expanded form with exponents. It means that ones place is represented by 100, tens place is represented by 101, hundreds place is represented by 102, and so on.

In essence, the expanded form in math (also called expanded notation) is a way to decompose a value into summands corresponding to its digits. When you write a number in expanded form (also know as expanded notation), you are expressing the number separated into its composite individual place values (and decimal values if necessary) in the form of an expression. Whenever we take some integer power of 10 (we're not considering fraction exponents here), the result is the digit 1 with several zeros that corresponds to that power. So what is expanded form? 1 is in the ones column and so, it is just worth 1. Note how the use of a place value chart can help you write numbers in expanded form. greatschools Count the number of places that each digit is to the right of the decimal point to see how many zeros are in the fraction it is out of. 83, Now, the expanded form 34 is written as 3(1/10) + 4(1/100) [As 3 represents the tenth position and 4 represents the hundredth position], Thus, the expanded form of 83.34 is written as 80+3+(3/10)+(4/100). We can add the values of the digits to get the number. Your Mobile number and Email id will not be published. In this article, we are going to discuss the expanded form of the number, expanded form of decimal numbers, expanded factor form, expanded exponential form with many solved examples in detail. b) 2414, Learn All About Writing Numbers In Expanded Notation. Here is another example writing decimals in the expanded form. Write 25.25 decimal in expanded form. We welcome your feedback, comments and questions about this site or page. 4987.56 A keen eye may have noticed a common thread when writing numbers in expanded form (even the expanded form with decimals): it's all about adding zeros in the right places. Write the number according to the place value and multiply the digits. The expanded form of the number 5367 is 5000+300+60+7. Write the following numbers in Expanded Form of Decimal Fractions In the next example we write 0.503 in expanded form. Click here to download this chart as an easy-to-print PDF file.. Scroll down the page for examples and solutions.

In this case, there's one such (namely, a), so we have b = a0 (remember that here we use the notation of writing digit after digit). Digits to the right of the decimal point are less than one and are written as fractions. The expanded form of 10,000 is 10000+0+0+0+0. We will write this decimal in expanded form. An easy way of thinking about writing numbers in expanded form is taking apart a number into its specific place values. On the other hand, we find d-s by putting as many zeros on the left side of c-s as we have digits between the decimal dot and the digit in question. Notice that we only have two non-zero digits in 0.37: 3 and 7. = 100 + 50 + 6 + $\frac{2}{10}$ + $\frac{4}{100}$ Exponents of 10 are very simple. = 2 10 + 5 1 . The expanded form of the numbers helps to determine the place value of each digit in the given number.

The 1 is in the ones column and is simply written as 1. Whereas the expanded form of the number is the separation of individual digits with their place value. 1 Digits(Tenths) Let's take a number that has the form aaaaaa, i.e., the a-s denote consecutive digits of the number with a being the ones digit, a the tens digit, and so on. Therefore we only have two numbers in our expanded form answer. Expand the decimal number 3.726 in the exponential form. How To Write Numbers In Expanded Notation? ii. Solution: The next example of writing decimals in expanded form is 0.37. = 4000 + 900 + 80 + 7 + $\frac{5}{10}$ + $\frac{6}{100}$ The framework from the first section doesn't change: the expanded form with decimals should still give us a sum of the form: aaaaaa.cccc = b + + b + b + b + b + b + d + d + d + + d. = 1 1000 + 0 100 + 0 10 + 0 1 + 4 $\frac{1}{10}$ + 2 $\frac{1}{100}$

Example: 111.12= 1 hundreds + 1 tens + 1 ones + decimal point + 1 tenths + 2 hundredths Or spending way too much time at the gym or playing on my phone. The expanded form splits the number, and it represents the number in units, tens, hundreds and thousands form. The 3 is in the tenths column and so it is worth 3 tenths, 3 / 10 . Example: Write the decimal 0.5 into a fraction.

NCERT Solutions Class 12 Business Studies, NCERT Solutions Class 12 Accountancy Part 1, NCERT Solutions Class 12 Accountancy Part 2, NCERT Solutions Class 11 Business Studies, NCERT Solutions for Class 10 Social Science, NCERT Solutions for Class 10 Maths Chapter 1, NCERT Solutions for Class 10 Maths Chapter 2, NCERT Solutions for Class 10 Maths Chapter 3, NCERT Solutions for Class 10 Maths Chapter 4, NCERT Solutions for Class 10 Maths Chapter 5, NCERT Solutions for Class 10 Maths Chapter 6, NCERT Solutions for Class 10 Maths Chapter 7, NCERT Solutions for Class 10 Maths Chapter 8, NCERT Solutions for Class 10 Maths Chapter 9, NCERT Solutions for Class 10 Maths Chapter 10, NCERT Solutions for Class 10 Maths Chapter 11, NCERT Solutions for Class 10 Maths Chapter 12, NCERT Solutions for Class 10 Maths Chapter 13, NCERT Solutions for Class 10 Maths Chapter 14, NCERT Solutions for Class 10 Maths Chapter 15, NCERT Solutions for Class 10 Science Chapter 1, NCERT Solutions for Class 10 Science Chapter 2, NCERT Solutions for Class 10 Science Chapter 3, NCERT Solutions for Class 10 Science Chapter 4, NCERT Solutions for Class 10 Science Chapter 5, NCERT Solutions for Class 10 Science Chapter 6, NCERT Solutions for Class 10 Science Chapter 7, NCERT Solutions for Class 10 Science Chapter 8, NCERT Solutions for Class 10 Science Chapter 9, NCERT Solutions for Class 10 Science Chapter 10, NCERT Solutions for Class 10 Science Chapter 11, NCERT Solutions for Class 10 Science Chapter 12, NCERT Solutions for Class 10 Science Chapter 13, NCERT Solutions for Class 10 Science Chapter 14, NCERT Solutions for Class 10 Science Chapter 15, NCERT Solutions for Class 10 Science Chapter 16, NCERT Solutions For Class 9 Social Science, NCERT Solutions For Class 9 Maths Chapter 1, NCERT Solutions For Class 9 Maths Chapter 2, NCERT Solutions For Class 9 Maths Chapter 3, NCERT Solutions For Class 9 Maths Chapter 4, NCERT Solutions For Class 9 Maths Chapter 5, NCERT Solutions For Class 9 Maths Chapter 6, NCERT Solutions For Class 9 Maths Chapter 7, NCERT Solutions For Class 9 Maths Chapter 8, NCERT Solutions For Class 9 Maths Chapter 9, NCERT Solutions For Class 9 Maths Chapter 10, NCERT Solutions For Class 9 Maths Chapter 11, NCERT Solutions For Class 9 Maths Chapter 12, NCERT Solutions For Class 9 Maths Chapter 13, NCERT Solutions For Class 9 Maths Chapter 14, NCERT Solutions For Class 9 Maths Chapter 15, NCERT Solutions for Class 9 Science Chapter 1, NCERT Solutions for Class 9 Science Chapter 2, NCERT Solutions for Class 9 Science Chapter 3, NCERT Solutions for Class 9 Science Chapter 4, NCERT Solutions for Class 9 Science Chapter 5, NCERT Solutions for Class 9 Science Chapter 6, NCERT Solutions for Class 9 Science Chapter 7, NCERT Solutions for Class 9 Science Chapter 8, NCERT Solutions for Class 9 Science Chapter 9, NCERT Solutions for Class 9 Science Chapter 10, NCERT Solutions for Class 9 Science Chapter 11, NCERT Solutions for Class 9 Science Chapter 12, NCERT Solutions for Class 9 Science Chapter 13, NCERT Solutions for Class 9 Science Chapter 14, NCERT Solutions for Class 9 Science Chapter 15, NCERT Solutions for Class 8 Social Science, NCERT Solutions for Class 7 Social Science, NCERT Solutions For Class 6 Social Science, CBSE Previous Year Question Papers Class 10, CBSE Previous Year Question Papers Class 12. The number of places each digit is to the right of the decimal point is the same as the number of zeros in the. For better understanding let us expand each of the digits in the place value. The number of places each digit is to the right of the decimal point is the number of zeros in the. To make it more precise, let's have it neatly described in a separate section. Decimal in the expanded form is similar to the integer expanded form. Fortunately, we obtain b-s similarly as before; we just have to remember to take the dot into account. The digit 1 is one place to the right of the decimal point and so the number on the bottom of the fraction contains 1 zero. = 900 + 60 + 6 + $\frac{6}{10}$ + $\frac{3}{100}$, Example 3. This means our expanded form answer is made up of three numbers added together. What is the expanded form of such a monstrosity? Remember that we only write the values of non-zero digits.

If You Experience Display Problems with Your Math Worksheet. Write the tens: 0 as 0 10 The expanded form of 2567 is 2. 3. These Expanded Form with Decimals Worksheets are great for testing children on writing numbers out in expanded form that include decimals. iii. To write the expanded form with decimals first you have to know what is expanded form, place value system, etc. We only consider the digits that are not zero. Here we observe that there is one number after the point. 45.12 = 4 10 + 5 1 + 1 $\frac{1}{10}$ + 2 $\frac{1}{100}$ To be precise, we add as many zeros as we have digits to the right, but before the decimal dot (i.e., we only count the a-s). 1.089 is written in expanded form as 1 + 8 / 100 + 9 / 1000 . Solution: In the number 10,000, there are zero thousand, zero hundred, zero tens and zero ones. 45.12 = 4 tens + 5 ones + decimal point + 1 tenths + 2 hundredths Write 1000.42 in Expanded form with decimals. Let's explain how to write such numbers in expanded form starting from the right side, i.e., from a.

Anthony is the content crafter and head educator for YouTube'sMashUp Math. iii. How to write decimal numbers in expanded notation? Well, you add zeros. The 3 is in the tenths column and so, it is worth 3 tenths. Example: Some of the examples of the expanded form of numbers are provided in the tabular form: Let us take the number 723.

In fact, any number raised to power 0 equals 1. We ignore the 0 in the ones column because it is not worth anything. = 4 thousands + 9 hundreds + 8 tens + 7 ones + decimal point + 5 tenths + 6 hundredths Digits after the decimal point are worth less than one whole. In number 723, there are 7 hundreds, 2 tens and 3 ones. The 1 is in the thousandths column and is worth 1 thousandth, 1 / 1000 . The 9 is in the thousandths column and is written as.

Step 2: Identify the place value of the given number using the place value chart. The 1 is in the tenths column and so is worth 1 tenth. 111.12 = 1 100 + 1 10 + 1 1 + 1 $\frac{1}{10}$ + 2 $\frac{1}{100}$ Decimals are a short way to write the fractions and mixed fractions.

3 Digits(Thousandths).

5 is in the one column and so is just worth 5. Similarly, to b we'll add two zeros (since a has a and a to the right), meaning that b = a00, and so on until b = a00000 with n-1 zeros. So how do you write a number in expanded form when it has some fractional part?

The decimal numbers can also be written in the expanded form. 156.24 = 100 + 50 + 6 + 0.2 + 0.04, Learn how to write decimals in expanded form from the below. The perfect snowman calculator uses math & science rules to help you design the snowman of your dreams!

Post Views: 1